F1 Drivers Height Weight 2020

Empty Message

Volume Of A Sphere With A Radius Of 3 In Terms Of Pi

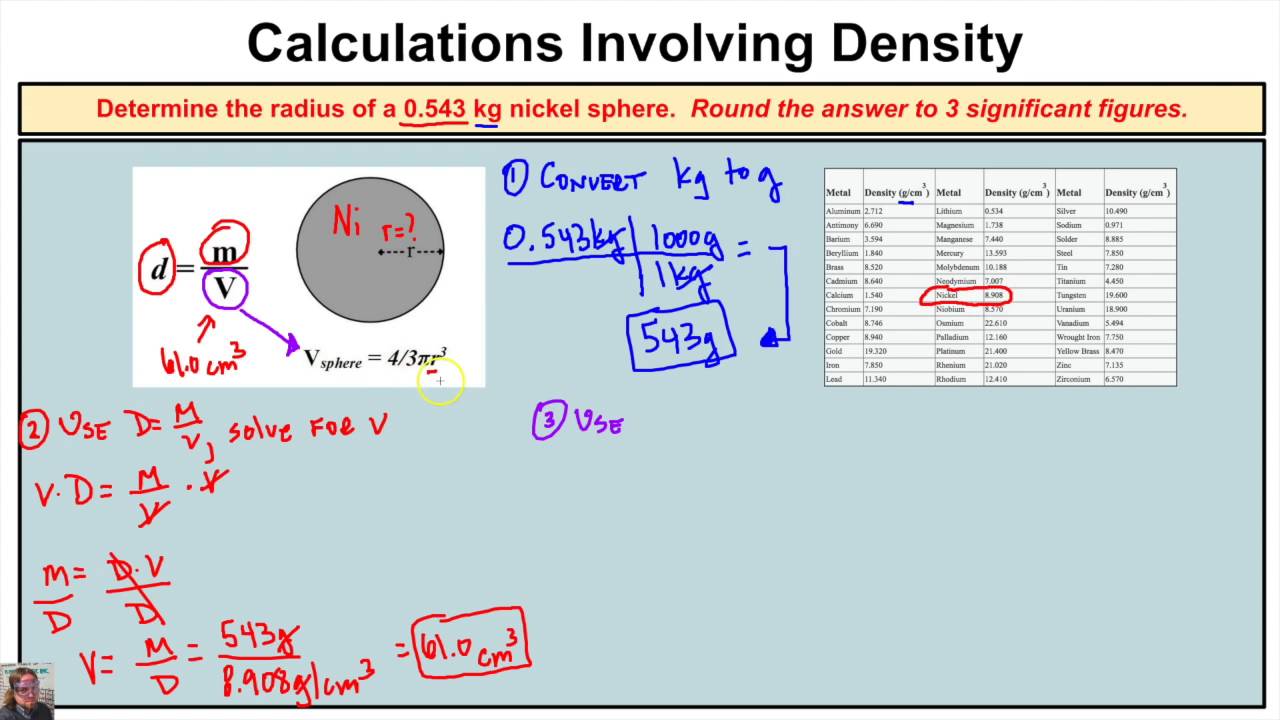
The unit of volume of a sphere is given as the 3. The metric units of volume are cubic meters or cubic centimeters while the USCS units of volume are, cubic inches or cubic feet. The volume of sphere depends on the radius of the sphere, hence changing it changes the volume of the sphere. There are two types of spheres, solid sphere, and hollow sphere.

The volume of both types of spheres is different. We will learn in the following sections about their volumes. Volume is the quantification of the three-dimensional space a substance occupies. The SI unit for volume is the cubic meter, or m3.

Volumes of many shapes can be calculated by using well-defined formulas. In some cases, more complicated shapes can be broken down into simpler aggregate shapes, and the sum of their volumes is used to determine total volume. The volumes of other even more complicated shapes can be calculated using integral calculus if a formula exists for the shape's boundary.

Beyond this, shapes that cannot be described by known equations can be estimated using mathematical methods, such as the finite element method. Alternatively, if the density of a substance is known, and is uniform, the volume can be calculated using its weight. This calculator computes volumes for some of the most common simple shapes. If you ever wondered what's the volume of the Earth, soccer ball or a helium balloon, our sphere volume calculator is here for you. It can help to calculate the volume of the sphere, given the radius or the circumference. Also, thanks to this calculator you can determine the spherical cap volume or hemisphere volume.

Calculating volume and surface area of sphere play an important role in mathematics and real life as well. Formulas for volume & surface area of sphere can be used to explore many other formulas and mathematical equations. In geometry, a spherical cap or spherical dome is a portion of a sphere or of a ball cut off by a plane. It is also a spherical segment of one base, i.e., bounded by a single plane. If the plane passes through the center of the sphere, so that the height of the cap is equal to the radius of the sphere, the spherical cap is called a hemisphere.

The volume of sphere is the capacity it has. It is the space occupied by the sphere. The volume of sphere is measured in cubic units, such as m3, cm3, in3, etc. The shape of the sphere is round and three-dimensional. It has three axes as x-axis, y-axis and z-axis which defines its shape. All the things like football and basketball are examples of the sphere which have volume.

A sphere is the shape of a basketball, like a three-dimensional circle. Just like a circle, the size of a sphere is determined by its radius, which is the distance from the center of the sphere to any point on its surface. The formulas for the volume and surface area of a sphere are given below. A glass dome for a lighting fixture is in the shape of a hemisphere.

The circumference of the great circle of the hemisphere is 12π inches. Which statements about the hemisphere are true? The total surface area is 108π square inches. The total surface area is 144π square inches.

The total surface area is 432π square inches. The total surface area is 36π square inches. In this lesson, you'll learn how to find the volume of a sphere with a radius of 4 inches.

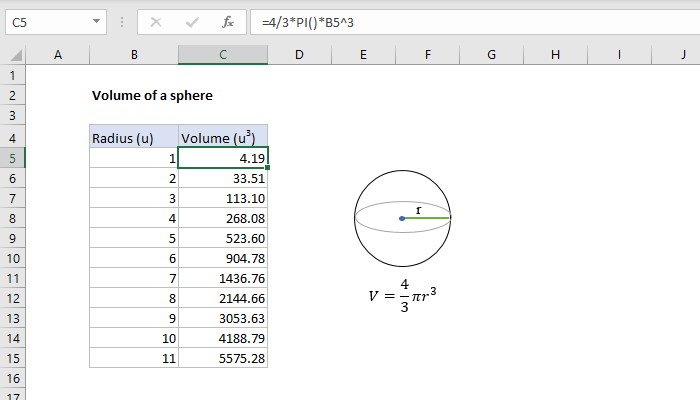
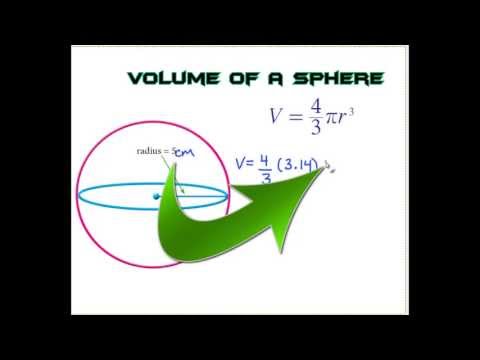
A sphere is a 3-dimensional round object. The volume is how space is inside the sphere. When you want to find out how much space is inside such a sphere, you'll follow these steps to calculate the volume of the sphere. Note- In order to solve this question, we must know the formula of volume of sphere i.e. $\dfrac\pi $.

Along with that formula, we must know all the formulas of a sphere like total surface area i.e. $4\pi $ to solve similar kinds of problems. A sphere is a three-dimensional, round object, such as a marble or soccer ball. The volume represents the space enclosed by the object. The formula for the volume of a sphere is 4/3 times pi times the radius cubed. Cubing a number means multiplying it by itself three times, in this case, the radius times the radius times the radius. To find the volume in terms of pi, leave pi in the formula rather than converting it to 3.14.

A sphere is a three-dimensional solid with no face, no edge, no base and no vertex. It is a round body with all points on its surface equidistant from the center. The volume of a sphere is measured in cubic units. A sphere is a three-dimensional solid with no base, no edge, no face and no vertex. Sphere is a round body with all points on its surface equidistant from the center.

In this example you need to calculate the volume of a very long, thin cylinder, that forms the inside of the pipe. The area of one end can be calculated using the formula for the area of a circle πr2. The diameter is 2cm, so the radius is 1cm. The area is therefore π × 12, which is 3.14cm2.

Now the question becomes calculating the volume of the bicylinder . It is also very difficult, so add a cube packing the bicylinder . Now when the plane intersects the cube, it forms another larger square. The extra area in the large square , is the same as 4 small squares . Moving through the whole bicylinder generates a total of 8 pyramids. This online calculator will calculate the 3 unknown values of a sphere given any 1 known variable including radius r, surface area A, volume V and circumference C.

It will also give the answers for volume, surface area and circumference in terms of PI π. A sphere is a set of points in three dimensional space that are located at an equal distance r from a given point . For any other value for the length of the radius of a sphere, just supply a positive real number and click on the GENERATE WORK button. They can use these methods in order to determine the surface area and volume of parts of a sphere. There is another special formula for finding the volume of a sphere. The volume is how much space takes up the inside of a sphere.

The answer to a volume question is always in cubic units. This statement is not at all obvious or elementary. "A sphere's volume is two cones of equal height and radius to that of the sphere's".

The assertion about the cone and the cylinder is a little easier to prove, but it too is not obvious. So you have not really provided an answer to this to year old question. I think the accepted answer is closest to what you have in mind. If you want to help here I think you should pay attention to new questions that don't yet have answers. A set of points in a space equally distanced from a given point $O$ is a sphere. The point $O$ is called the center of the sphere.

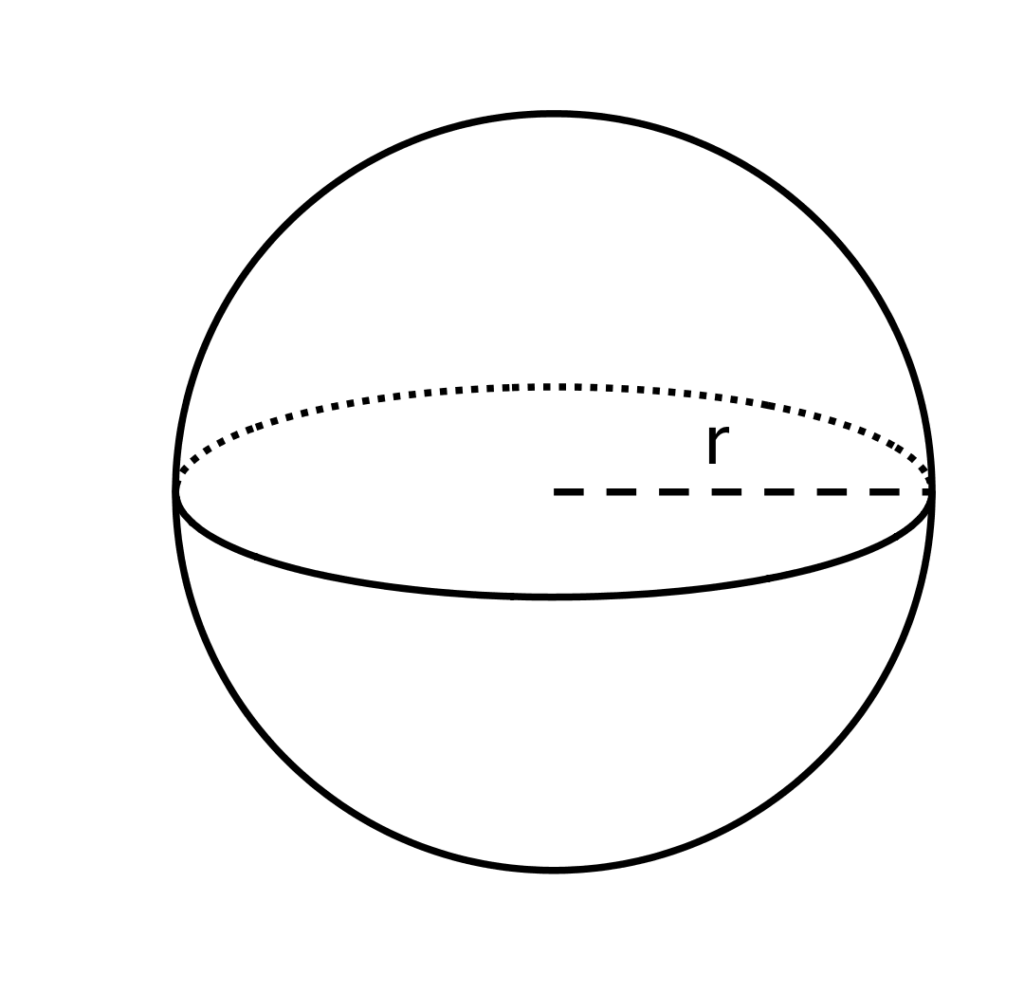
The distance from the center of a sphere to any point on the sphere is called the radius of this sphere. A radius of a sphere must be a positive real number. The segment connecting two points on the sphere and passing through the center is called a diameter of the sphere. All radii of the sphere are congruent to each other. A sphere can be obtained by rotating a semicircle about the diameter.

Two spheres of the same radius are congruent. The following video shows how to solve problems involving the formulas for the surface area and volume of spheres. If the baseball has a surface area of 9π, then I can set that equal to the formula 4πr2 and solve for r. The radius is 3/2 inches, so I double that to find the diameter.

The diameter of the ball is 3 inches, which is greater than the allowed range of diameters. A regulation baseball must have a diameter between 2.87 and 2.94 inches. The surface area of a particular baseball is 9π square inches.

Is the baseball within the range of regulation size? The volume of a sphere is the measurement of the space it can occupy. A sphere is a three-dimensional shape that has no edges or vertices. In this short lesson, we will learn to find the volume of a sphere, deduce the formula of volume of a sphere and learn to apply the formulas as well.

Once you understand this chapter you will learn to solve problems on the volume of the sphere. The volume of a sphere is the amount of space occupied by it. For a hollow sphere like a football, the volume can be viewed as the number of cubic units required to fill up the sphere. A sphere is defined as the set of all points in three-dimensional Euclidean space that are located at a distance (the "radius") from a given point (the "center"). Twice the radius is called the diameter, and pairs of points on the sphere on opposite sides of a diameterare called antipodes. When a sphere is cut by a plane that passes through its center, the intersection of the sphere and the plane is called a great circle.

Another way to think of this is that a great circle of a sphere is a circle that cuts the sphere exactly in half, forming two hemispheres. This means that the radius of the great circle will also be the radius of the sphere . Let us see some examples of calculating the volume of spheres of different dimensions. Volume is the amount of total space on the interior of the solid. Knowing the definition of volume, we can now focus on the formulas for volume of common geometric solids.

Using these formulas manually won't be difficult, but for fast, accurate results every time, use the volume calculator. The volume of a 3 -dimensional solid is the amount of space it occupies. Be sure that all of the measurements are in the same unit before computing the volume.

For example, if the radius of your sphere equals 19 inches, multiply 19 by 19 to get 361 square inches. The volume of a sphere is measured in cubic units, i.e., m3, cm3, in3, ft3, etc. The sphere is an extended version of a circle. Or it will be right to say a 3D version of a circle. In geometry, a sphere is a 3-dimensional round solid figure in which every point on its surface is equidistant from its center.

This concept can be of significance in geometry, to find the volume & surface area of sphere and its parts. Real life problems on volume & surface area of sphere are very common, so this concept can be of great importance of solving problems. Any cross section of a sphere by a plane is a circle.

The circle obtained as a cross section of the sphere and plane through the center of the sphere is called a great circle. Any plane that passes through the center $O$ of a sphere divides it into two congruent parts well-known as hemispheres. Bunuel For the volume of the sphere why are we taking "outer radius 5r" and "inner radius 2r" for the volume of the empty space? I can't identify it from the pic which one is the inner or outer radius, which one is solid sphere and spherical shell. In the imperial/English system the equivalent measurements are fluid ounces, pints, quarts and gallons, which are not easily translated into cubic feet.

It is therefore best to stick to either liquid or solid volume units. Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations. The volume of a hemisphere is equal to two-thirds of the product of pi and the cube of the radius. 7Given a solid sphere of radius R, remove a cylinder whose central axis goes through the center of the sphere.

Volume Of A Sphere With A Radius Of 3 Browse other questions tagged geometry volume solid-geometry spheres or ask your own question. Well I wasn't really going for elementary, just a dumbed down version that worked for me that might help others starting at University Math. The other answers were great with backgrounds of why a sphere fits into a cylinder, etc, so I left that part out of mine. I personally wasn't able to figure out where 4/3 came from using any of their answers, so I contributed mine to help those that may see things my way.

I agree it is an old question, but I had this question in 2019 that I couldn't find the answer to with those answers. Assume that the volume of the sphere is made up of numerous thin circular disks which are arranged one over the other as shown in the figure given above. The circular disks have continuously varying diameters which are placed with the centres collinearly. A thin disk has radius "r" and the thickness "dy" which is located at a distance of y from the x-axis.